摆锤

此环境是经典控制环境的一部分，其中包含有关该环境的一般信息。

动作空间	Box(-2.0, 2.0, (1,), float32)
观测空间	Box([-1. -1. -8.], [1. 1. 8.], (3,), float32)
导入	gymnasium.make("Pendulum-v1")

描述

倒立摆上摆问题基于控制理论中的经典问题。该系统由一个摆锤组成，一端连接到固定点，另一端自由。摆锤从随机位置开始，目标是对自由端施加扭矩，使其摆动到直立位置，重心恰好位于固定点正上方。

下图详细说明了用于实现摆锤动力学方程的坐标系。

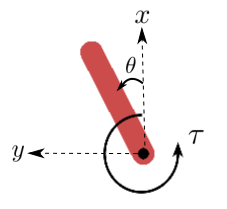
• x-y：摆锤末端以米为单位的笛卡尔坐标。

• theta ：以弧度表示的角度。

• tau：以牛顿米（N m）表示的扭矩。定义为正值表示逆时针方向。

动作空间

动作是一个形状为 (1,) 的 ndarray，表示施加到摆锤自由端的扭矩。

编号	动作	最小值	最大值
0	扭矩	-2.0	2.0

观测空间

观测值是一个形状为 (3,) 的 ndarray，表示摆锤自由端的 x-y 坐标及其角速度。

编号	观测值	最小值	最大值
0	x = cos(theta)	-1.0	1.0
1	y = sin(theta)	-1.0	1.0
2	角速度	-8.0	8.0

奖励

奖励函数定义为

r = -(theta² + 0.1 * theta_dt² + 0.001 * torque²)

其中 theta 是摆锤在 [-pi, pi] 之间归一化后的角度（0 表示直立位置）。根据上述方程，可以获得的最小奖励为 -(pi² + 0.1 * 8² + 0.001 * 2²) = -16.2736044，而最大奖励为零（摆锤直立，速度为零，未施加扭矩）。

初始状态

初始状态是 [-pi, pi] 范围内的随机角度和 [-1,1] 范围内的随机角速度。

剧集截断

剧集在 200 个时间步后截断。

参数

• g: .

摆锤在 gymnasium.make 中有两个参数：render_mode 和 g，其中 g 表示用于计算摆锤动力学的重力加速度（单位为 m s^-2）。默认值为 g = 10.0。在重置时，options 参数允许用户更改用于确定新随机状态的边界。

>>> import gymnasium as gym
>>> env = gym.make("Pendulum-v1", render_mode="rgb_array", g=9.81)  # default g=10.0
>>> env
<TimeLimit<OrderEnforcing<PassiveEnvChecker<PendulumEnv<Pendulum-v1>>>>>
>>> env.reset(seed=123, options={"low": -0.7, "high": 0.5})  # default low=-0.6, high=-0.5
(array([ 0.4123625 ,  0.91101986, -0.89235795], dtype=float32), {})

版本历史

• v1: 简化数学方程，行为无差异。

• v0: 初始版本发布